Fortunes Algorithm (Part 2): Some implementation details

In my previous post, I gave an overview of how Fortune’s algorithm works. For simplicity’s sake I specifically left out details about implementation and so we’ll cover some of that in this post instead.

I spent far longer than I originally intended trying to write my own implementation. The main reason for this is that I was repeatedly delayed by the discovery of yet another edge-case which caused my implementation to fail. The goal of this post is to detail those edge-cases that I managed to fix, and describe as best I can those which I did not.

Before we get into that however, there is one detail that I left out which is not an edge case and is actually rather fundamental:

How should the beachline be stored in memory?

Our beachline needs to support three main operations: Insertion, deletion and lookup by x-coordinate. If performance is not a concern then you can use whatever you like. I originally used a linked list. Since nothing ever moves once its been inserted into the beachline (by which I mean that beachline never gets re-ordered), I originally linked list and simply inserted items in the correct place. This meant that searching, inserting and deleting were all O(n) but when you have 15 data points that’s fine.

For better performance we’d like to at least improve the lookup time. There are multiple ways of doing this. One way that I’ve seen is to bucket the items in the beachline by x-coordinate and then just do a linear search through the correct bucket. You could also just use a generic implementation of some self-balancing tree.

For my implementation I used a tree structure suggested in Ivan Kutskir’s post, attributed to Steven Fortune himself. The basic idea of this tree is that all leaf nodes are arcs and all internal nodes are edges. The tree is such that an in-order traversal will list the items in left-to-right order as they appear at the beachline.

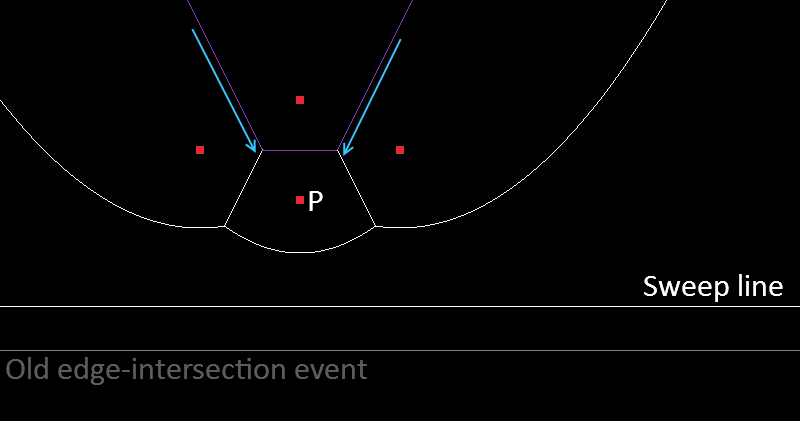
Since its a tree the lookup is pretty straightforward, its just the usual decide-which-branch-to-take-and-recurse approach. The only time anything gets inserted into the beachline is when we encounter a new site and at that point we insert 5 items (a left and right arc and edge, and a new arc in the middle) as shown below:

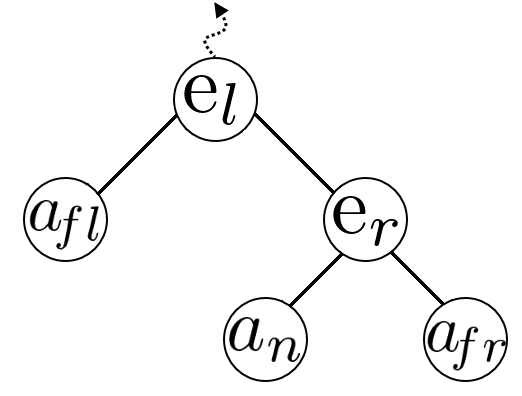
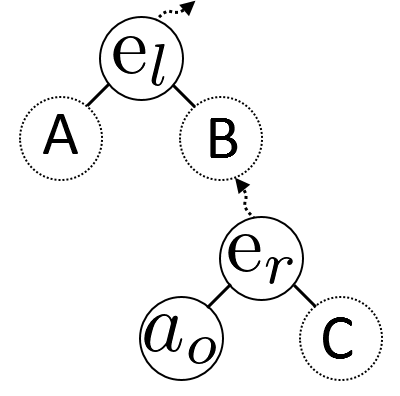
Removal is a little more complicated. The only time anything gets removed from the beachline is when we encounter an edge-intersection event and at that point we remove 3 items (an arc and the edge on either side of it). Now because of the way we insert items, both edges must be a (grand)parent of the arc that we want to remove and in particular, one of them must be that arc’s immediate parent.

Before we remove the arc’s parent, we need to first do something with it’s sibling. So we’ll put it in it’s parent’s place as one of it’s parent’s parent’s children. We can then safely remove the arc and parent edge from the tree, but there is another parent somewhere higher up the tree. This higher edge simply gets substituted with the new replacement edge, inheriting the same parent and children.

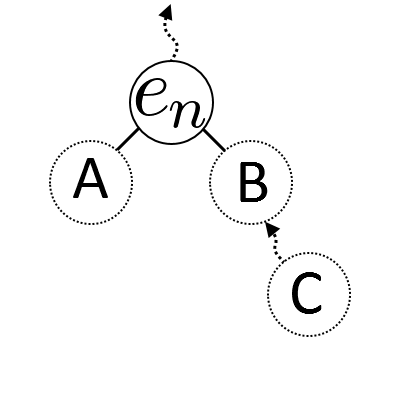
Edge cases

While attempting to write my own implementation, I encountered quite a number of edge-cases. I suppose this is not unsurprising for a geometric algorithm such as Fortune’s but nonetheless they were the cause of much headache. Below are some edge-cases to look out for, along with how I handled them.

Edge case 1: First two points have (almost) the same y-coordinate

During the normal running of the algorithm, any time we encounter a new site we first need to find the existing arc that covers that new site’s x-coordinate. This is a problem if there are no existing arcs or if none of those that exist measurably cover the required x-coordinate.

During initialization we start by just adding the first arc to the beachline. This is always going to be necessary so we may as well do it anyways, I don’t consider this to be an edge-case really. However if the first two arcs have the exact same y-coordinate, then when we arrive (via the standard code-path) at the lookup for the second one, the first arc is still just a straight vertical line. Straight vertical lines don’t cover very many x-coordinates, so you run into trouble when you try to find the intersection of what turns out to be two parallel straight lines.

To solve this, I added an extra case during startup that takes all points that are close enough in y to the first one (my cutoff was a difference of 1.0) and adds them to the beachline. The reason I used a cutoff of 1.0 and not something significantly smaller is that even with points that differ by 0.5, the parabola that is produced when the directrix is so close to the focus is exceptionally “narrow” (as much as such a word makes sense for something that extends out to infinity in x). This results in the function evaluating to a very large value and the resulting loss of precision causes issues later on.

Another potential problem here is that we need to select a y-coordinate for the starting point of the edge (since we only need the edge to grow downwards). If you are working within a defined region then you could just use the largest possible y-value you have available. I was trying to avoid such a restriction so I originally tried using FLT_MAX, which leads to precision issues. In the end I just added a flag that gets set only on edges like this to indicate that the edge conceptually “extends out to positive infinity in y”.

Of course you could also ignore all of the above and just throw in a new site somewhere sufficiently far above all your other sites to ensure that this never happens to you.

Edge case 2: Multiple edge-intersection events are created for a single arc

When an edge-intersection event gets added to the event queue, it is not necessarily guaranteed to need to execute. It is entirely possible that an event gets added for the intersection of two edges that then intersect with something else before they intersect each other.

One way to solve this is to dig through the event queue when you remove arcs from the beachline and clean out any intersection events that are no longer needed. I think it’s simpler to just add a flag on the edge-intersection event to indicate whether or not the event is still valid. If the event gets pulled from the queue and is not valid then it simply gets ignored.

In the case of C++ (or anything else where you have to manage your own memory) you also have a related issue of when to clean up. Having a flag to invalidate the event means that I can delete the arcs and edges that are no longer needed and know that they won’t be referenced by some event later on.

Edge case 3: Precision issues with determining intersections of curves (Unsolved)

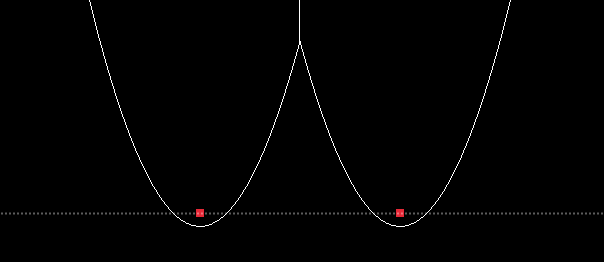
One issue that I was not able to solve, was that the code that finds the intersection between a parabola and an edge is sometimes slightly off when the two are very close together. I’m finding intersections by just subtracting the edge’s equation from the parabola’s equation and solving via the quadratic formula. This works analytically but in practice I get a value like 2e-10 instead of 0 under the square root sometimes and so it claims that things don’t intersect when actually they should.

The easiest place to see this is on the first demo in the previous post. If you hold your mouse exactly over the 3rd site from the top, you get the following:

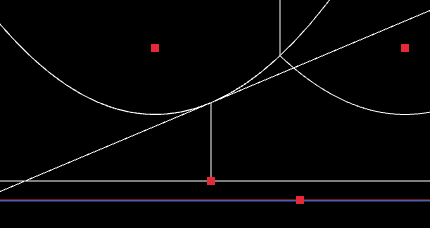
This happens because the code for rendering each edge and arc tries to find the extents of each item. It finds that the edge and the arc do not intersect and so draws the full width of them both.

I found it helpful when trying to resolve this sort of issue, to generate many random points and have them move around to see what happens. The below demo has 800 points, randomly placed, each moving in a random direction. I’m sure it’ll only take a few seconds of watching this for you to see some cases where the output is incorrect (the long edges across the screen that show up for a few frames at a time).

Conclusion

That’s it for my exploration of fortune’s algorithm. It’s been both interesting and frustrating, I would liked to have arrived at a bug-free implementation but oh well. If you’re interested, you can find my source code here. A 64-bit windows binary of the previous post’s demo is also available here.